比赛利器：陈天奇的XGBoost

XGBoost

Index

XGBoost背景
XGBoost与传统GBDT的区别
常用的符号表示
泰勒公式
XGBoost中的目标函数
XGBoost的树生成过程
- Basic Exact Greedy Algorithm
- Approximate Algorithm
XGBoost的稀疏处理
XGBoost的工程设计
- Column Blocks and Parallelization
- Cache Aware Access
如何上手XGBoost
- 超参数配置
- demo代码
相关引用

背景

2014 年 3 月，XGBOOST 最早作为研究项目，由陈天奇提出。2016年，相关的论文《XGBoost: A Scalable Tree Boosting System》发表在KDD。XGBoost展开的意思就是Extreme Gradient Boosting，其中Extreme代表极致。工程设计层面的极致包括贪心的排序操作、分割点近似、并发的程序执行；算法层面的极致包括二阶导数、决策树正则项的使用等。本篇博客将会介绍一下几个方面：

XGBoost与传统GBDT的区别
常用的符号表示
泰勒公式
XGBoost中的目标函数（二阶导数）
XGBoost中的优化方法
XGBoost中的正则项
XGBoost中节点的split方法
XGBoost的并行
如何上手XGBoost

XGBoost与传统GBDT的区别

注意：这里所比较的GBDT是以CART作为基分类器的回归树

传统GBDT以CART作为基分类器。XGBoost还支持线性分类器（gbtree和gblinear），这个时候XGBoost相当于带L1和L2正则化项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）。
传统GBDT在优化时只用到一阶导数信息，XGBoost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。顺便提一下，XGBoost工具支持自定义代价函数，只要函数可一阶和二阶求导。
XGBoost在代价函数里加入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。从Bias-variance tradeoff角度来讲，正则项降低了模型的variance，使学习出来的模型更加简单，防止过拟合，这也是XGBoost的优点。
Shrinkage（缩减），相当于学习速率（XGBoost中的eta）。XGBoost在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间。实际应用中，一般把eta设置得小一点，然后迭代次数设置得大一点。（补充：传统GBDT的实现也有学习速率）
列抽样（column subsampling）。XGBoost借鉴了随机森林RF的做法，支持列抽样（选择部分特征），不仅能降低过拟合，还能减少计算，这也是XGBoost异于传统GBDT的一个特性。
对缺失值的处理。对于特征的值有缺失的样本，xgboost可以自动学习出它的分裂方向。
XGBoost工具支持并行。Boosting不是一种串行的结构吗?怎么并行的？注意XGBoost的并行不是tree粒度的并行，xgboost也是一次迭代完才能进行下一次迭代的（第t次迭代的代价函数里包含了前面t-1次迭代的预测值）。XGBoost的并行是在特征粒度上的。决策树的学习最耗时的一个步骤就是对特征的值进行预排序（因为要确定最佳分割点），XGBoost在训练之前，预先对数据进行了排序，然后保存为block结构，后面的迭代中重复地使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。
可并行的近似直方图算法。树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost还提出了可并行的近似直方图算法，用于高效地生成候选的分割点。

常用的符号表示

符号	含义
$d$	特征数个数
$n$	样本个数
$R^d$	特征数为 $d$ 的数据集
$x_i \in R^d$	第 $i$ 个样本
$w_j$	第 $j$ 个特征的权重
$\widehat{y_i}$	$x_i$ 的预测值
$\Theta$	特征权重的集合, $\Theta={\{w_j\|j=1, \cdots ,d\}}$
$T$	叶子节点个数

泰勒公式

泰勒公式是一个用函数在某点的信息描述其附近取值的公式，可以理解为局部有效性。其基本形式如下：

$\begin{equation} f(x) = \sum\limits_{n=0}^{\infty} \frac{f^{(n)} (x_0)}{n!} {(x-x_0)}^{n} \end{equation}$

一阶泰勒展开： $f(x) \approx f(x_0) + f^{\prime} (x_0)(x-x_0)$
二阶泰勒展开： $f(x) \approx f(x_0) + f^{\prime} (x_0)(x-x_0) + f^{\prime\prime}(x_0) \frac{(x-x_0)^2}{2}$

假设$x^t = x^{t-1} + \Delta x$，将$f(x^t)$在$x^{(t-1)}$处进行泰勒展开，其迭代形式如下：

$\begin{aligned} f(x^t) & = f(x^{t-1} + \Delta{x}) \\ & \approx f(x^{t-1}) + f^{\prime}(x^{t-1}) \Delta{x} + f^{\prime\prime}(x^{t-1}) \frac{(\Delta x)^2}{2} \end{aligned}$

XGBoost中的目标函数

总体目标函数

$\begin{aligned} Obj = \begin{matrix} \underbrace{ \sum\limits_{i=1}^{n} L(y_i, \widehat{y_i}) } \\ {Training\ loss} \end{matrix} + \begin{matrix} \underbrace{ \sum\limits_{k=1}^{K} \Omega(f_k) } \\ {Regularization} \end{matrix} \end{aligned}$

第一项是针对 $n$ 个样本的 $Loss$, 它可以有多种选择
- 绝对值误差，$L(y_i, \widehat{y_i}) = |(y_i - \widehat{y_i})|$
- 平方误差，$L(y_i, \widehat{y_i}) = {(y_i - \widehat{y_i})}^2$，此时叫做gradient boosted machine
- logistic loss，$L(y_i, \widehat{y_i}) = y_i \ln(1 + \exp(-\widehat{y_i}) + (1-y_i)\ln(1+\exp(\widehat{y_i})))$，此时叫做logistBoost
第二项是正则项，即树的复杂度，下文重点分析。

Regularization

在XGBoost的目标函数中，$\Omega(f_t)$是代表模型的复杂度。这个部分在GBDT最初提出的时候并不完善，1999年Friedman的论文《GREEDY FUNCTION APPROXIMATION:A GRADIENT BOOSTING MACHINE》中更多的是依靠学习率和Boosting树的规模两个因素来进行模型选择。

first-regularization-gbdt

2014年，Rie Johnson和Tong Zhang在《Learning Nonlinear Functions Using Regularized Greedy Forest》针对目标函数中正则项的部分提出了较为全面的分析。后续，这些正则思想在XGBoost中也得到了进一步的应用，主要包括：

树的深度
最小叶子权重
叶子个数
叶子权重的平滑程度

这里，用叶子个数和叶子权重的平滑程度来形式化描述模型的复杂度，可以得到：

$\begin{equation} \Omega(f_t) = \gamma T + \frac{1}{2} \lambda \sum_{j=1}^{T} w_{j}^{2} \end{equation}$

上式中，第一项利用叶子个数$T$乘以一个收缩系数$\gamma$，第二项用L2范数来表示叶子权重的平滑程度。下图就是计算复杂度的一个示例。

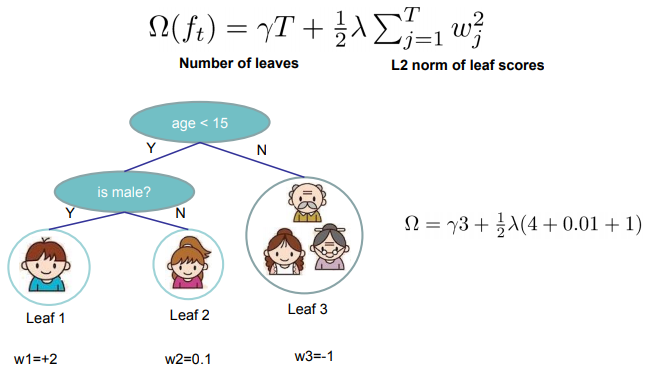
example-regularization-xgboost

Gradient Tree Boosting

假设我们有K棵树，根据Boosting的加法模型，那么：

$\begin{equation} \widehat{y_i} = \sum\limits_{k=1}^{K} f_k(x_i), f_k \in \boldsymbol{F} \end{equation}$

上式中$\boldsymbol{F}$表示的是回归森林中的所有函数空间；$f_k$表示一棵树，包括树的结构和叶子节点权重；$f_k(x_i)$表示的是第$i$个样本在第$k$棵树中落在自叶子的权重。以下图为例：

example-tree-ensemble

可见，男孩落在第一棵树的最左叶子和第二棵树的最左叶子，所以他的得分就是两个叶子节点的权重之和。

那么，我们需要求的参数就是每棵树的结构和叶子节点权重，简单来看就是$f_k$。用前面的符号表示进行结构统一，可以有：

$\begin{equation} \Theta= \{f_1, f_2, f_3 \cdots f_k\} \end{equation}$

注意，这里$\Theta$理解为所求参数的集合，里面的$f$和上文中的$w$本质上是一致的。这些参数都是未知待求解的，即下文目标函数和优化方法要求解的。

Boosting Tree的生成过程想法很简单，一棵树一棵树往上加，一直到K棵树停止。过程可以如下：

$\begin{cases} \widehat{y_i}^{(0)} = 0\\ \widehat{y_i}^{(1)} = f_1(x_i) = \widehat{y_i}^{(0)} + f_1(x_i)\\ \widehat{y_i}^{(2)} = f_1(x_i) + f_2(x_i) = \widehat{y_i}^{(1)} + f_2(x_i)\\ \cdots \\ \widehat{y_i}^{(t)} = \sum\limits_{k=1}^t f_k(x_i) = \widehat{y_i}^{(t-1)} + f_t(x_i)\\ \end{cases}$

其中，$\widehat{y_i}^{(t)}$表示第$t$次迭代后，样本$x_i$所得到的得分。

将上述定义好的Training Loss和Regularization带入目标函数，可得：

$\begin{aligned} Obj^{(t)} & = \sum\limits_{i=1}^{n} L(y_i, \widehat{y_i}^{(t)}) + \sum\limits_{i=1}^{t} \Omega(f_i) \\ & = \sum\limits_{i=1}^{n} L \left (y_i, \widehat{y_i}^{(t-1)} + f_t(x_i) \right ) + \Omega(f_t) + constant \\ \end{aligned}$

然后，应用泰勒公式进行二阶展开（这里不是xgboost最早提出，在Friedman 1999的论文里已经有了相关思想），将$\widehat{y_i}^{(t)}$看作$f(x + \Delta{x})$，$\widehat{y_i}^{(t-1)}$对应$f(x)$，$f_t(x_i)$对应$\Delta{x}$。

$\begin{aligned} f(x+\Delta x) \approx f(x) + f^{\prime}(x) \Delta{x} + \frac{1}{2} f^{\prime\prime}(x)(\Delta x)^2 \end{aligned}$

为了方便推导，这里做一些简单设定： $\begin{cases} g_i = f^{(\prime)}(x) = \frac{\partial L(y_i, \ \widehat{y_i}^{(t-1)})}{\partial \widehat{y_i}^{(t-1)}} \\ \ \\ h_i = f^{(\prime\prime)}(x) = \frac{\partial^{2} L(y_i, \ \widehat{y_i}^{(t-1)})}{\partial({\widehat{y_i}^{(t-1)}})^{2}} \end{cases}$

根据泰勒公式和 $g_i$ 和 $h_i$ 的设定，最终得到下式：

$\begin{aligned} Obj^{(t)} & = \sum\limits_{i=1}^{n} L \left ( y_i, \widehat{y_i}^{(t-1)} + f_t(x_i) \right ) + \Omega(f_t) + constant \\ & \approx \sum\limits_{i=1}^{n} \left [ L(y_i, \widehat{y_i}^{(t-1)}) + \begin{matrix} \underbrace{ \frac{\partial L(y_i, \ \widehat{y_i}^{(t-1)})}{\partial \widehat{y_i}^{(t-1)}} } \\ {g_i} \end{matrix} \begin{matrix} \underbrace{ f_t(x_i) } \\ {\Delta{x}} \end{matrix} + \frac{1}{2} \begin{matrix} \underbrace{ \frac{\partial^{2} L(y_i, \ \widehat{y_i}^{(t-1)})}{\partial({\widehat{y_i}^{(t-1)}})^{2}} } \\ {h_i} \end{matrix} \begin{matrix} \underbrace{ f_t^2(x_i) } \\ {(\Delta{x})^2} \end{matrix} \right ] + \Omega(f_t) + constant \\ & = \sum\limits_{i=1}^{n} \left [L(y_i, \widehat{y_i}^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i) \right ] + \Omega(f_t) + constant \\ & = \sum\limits_{i=1}^{n} \left [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i) \right ] + \Omega(f_t) + \left [\sum\limits_{i=1}^{n} L(y_i, \widehat{y_i}^{(t-1)}) + constant \right ] \end{aligned}$

很容易看出，上述公式中的第二部分 $\left [\sum\limits_{i=1}^{n} L(y_i, \widehat{y_i}^{(t-1)}) + constant \right ]$ 对于目标函数最优值的求解无任何影响（因为里面没有$f_t(x_i)$的相关信息），所以，现在把优化函数写作下面的形式：

$\begin{aligned} Obj^{(t)} \approx \sum\limits_{i=1}^{n} \left [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i) \right ] + \Omega(f_t) \end{aligned}$

我们已经知道，$f_t(x)$的物理意义（前文中的$f_k(x)$），它就是一棵树，重点是需要求解出它的参数，即树的结构和叶子节点权重，我们现在进一步形式化这棵树。设$w \in R^(T)$，$w$ 为树叶权重序列，$T$ 为叶子节点个数。$q\ :R^{(T)} \to {1,2, \cdots, T}$, $q$为树结构。那么$q(x)$表示的就是样本 $x$ 所落在树叶的位置。这里可以用下图简单的理解：

example-tree-structure

于是，$f_t(x)$可以用下式进行表示： $\begin{aligned} f_t(x) = w_{q(x)}, \ w \in R^T, \ q\ :R^{(T)} \to \{1,2, \cdots, T\} \end{aligned}$

最后，我们在增加一个定义，用 $I_j$ 来表示第j个叶子里的样本集合。也就是上图中，第 $j$ 个圈，就用 $I_j$ 来表示。

$\begin{aligned} I_j = \{i|\ q(x_i) = j\} \end{aligned}$

所以到目前位置，我们要求解的树模型就是关于这两个变量$I_j$和$w_j$（理解为，第 $j$ 棵树的结构和叶子节点权重），最终的优化函数可以针对这两个变量展开（舍弃常数项）：

$\begin{aligned} Obj^{(t)} & = \sum\limits_{i=1}^{n} \left [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i) \right ] + \Omega(f_t) + \left [\sum\limits_{i=1}^{n} L(y_i, \widehat{y_i}^{(t-1)}) + constant \right ] \\ & \approx \sum\limits_{i=1}^{n} \left [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i) \right ] + \Omega(f_t)\\ & = \sum\limits_{i=1}^{n} \left [g_i w_{q(x_i)} + \frac{1}{2} h_i {w_{q(x_i)}}^2 \right ] + \gamma T + \frac{1}{2} \lambda \sum_{j=1}^{T} w_{j}^{2}\\ & = \sum\limits_{j=1}^T \left [( \begin{matrix} \underbrace{ \sum_{i \in I_j} g_i } \\ {G_j} \end{matrix}) w_j + \frac{1}{2}( \begin{matrix} \underbrace{ \sum_{i \in I_j} h_i } \\ {H_j} \end{matrix} + \lambda) w_j^2 \right ] + \gamma T \\ & = \sum\limits_{j=1}^T \left (G_j w_j + \frac{1}{2} (H_j + \lambda) {w_j}^2 \right ) + \gamma T \end{aligned}$

XGBoost的树生成过程

到这里，问题已经很清晰了，我们要求这棵树$f_t(x)$，其实就是求解这两个变量$I_j$和$w_j$，那么如何求解呢，考虑两个问题？

如果已经得到了叶子节点$I_j$, 最小化$Obj^{(t)}$的$w_j$是多少？
如果将当前节点$I_j$分裂，应该选择哪个分裂点最小化$Obj^{(t)}$呢（这一步其实就是XGBoost中节点的split方法）？

上面两个问题本质上就是树$f_t(x)$的生成过程（树生成算法）：对根节点使用树节点的split方法，得到左子树$I_L$和右子树$I_R$，同时计算出左右子树叶子节点权重$w_L$和右子树$w_R$。对每个叶节点重复上述分裂过程，直到满足一定条件后退出，这棵树就生成完毕。

问题1：最小化$Obj^{(t)}$的$w_j$

$\begin{aligned} Obj^{(t)} = \sum\limits_{j=1}^T \left (G_j w_j + \frac{1}{2} (H_j + \lambda) {w_j}^2 \right ) + \gamma T \end{aligned}$

对公式中的$w_j$求导，令结果为零，容易求得：

$\begin{aligned} w_j^{*} = - \frac{G_j}{H_j + \lambda} \qquad j=1,2, \cdots, J. \end{aligned}$

此时最小的$Obj^{(t)}$是：

$\begin{aligned} {Obj^{(t)}}^{*} = - \frac{1}{2} \sum_{j=1}^{J} \frac{G_j^2}{H_j + \lambda} + \gamma T \end{aligned}$

问题2：XGBoost中节点的split方法

求解$I_j$和$w_j$不同，应为前者是对输入样本x所属空间的划分（树形结构），不连续，无法求导。精确对$I_j$进行分裂是个NP问题，所以贪心算法成为首选。即分裂某个节点时，只考虑对当前节点分裂后，哪个分裂方案能得到最小的$Obj^{(t)}$

如同传统决策树，CART中的办法也是遍历样本$x$的每个特征的每个分裂点，根据问题1计算$w_j^{}$和${Obj^{(t)}}^{}$。这个过程在XGBoost中有所优化（利用一些工程方法加速，如Cache和Column Blocks）

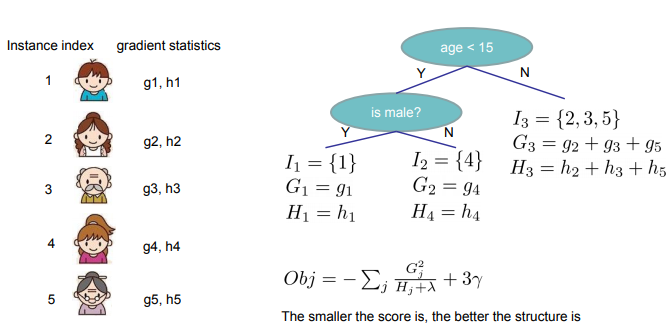
这个就是计算最优分割的示意图： example-optimization

[1]. Basic Exact Greedy Algorithm For SPLIT FINDING

从树的深度为0开始，每一个节点暴力遍历所有特征。对每个特征，先按照该特征里的值进行预排序，然后线性扫描来决定最好的分割点，最后在所有特征里选择分割后，Gain最高的那个特征。

$\begin{aligned} Obj_{split} &= -\frac{1}{2} \left[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda} \right]+\gamma T_split \\ Obj_{nosplit} &= -\frac{1}{2} \frac{(G_L+G_R)^2}{H_L+H_R+\lambda} + \gamma T_nosplit \\ \end{aligned}$ $\begin{aligned} Gain &= Obj_{nosplit} - Obj_{split} \\ &= -\frac{1}{2} \left[ \frac{G_L^2}{H_L+\lambda} + \frac{G_R^2}{H_R+\lambda} - \frac{(G_L+G_R)^2}{H_L+H_R+\lambda} \right] - \gamma (T_split - T_nosplit) \\ \end{aligned}$

这时，就有两种后续方法：

当Gain为负时就停止树的生长，这样效率比较高也简单，但也放弃了未来可能会有更好的情况。
一直分割到最大深度，然后进行修剪，递归地把划分叶子得到的Gain为负的收回。

一般来讲，方法2要好一些，于是我们采用后一种，完整算法如下：

Exact-Greedy-Algorithm-for Split-Finding

算法复杂度计算
1. 按照某个特征里的值进行排序，复杂度是$O(n*log{n})$
2. 扫描一遍该特征所有值，得到最优分割点，因为该层（兄弟节点一起考虑）一共有$n$个样本，所以复杂度是$O(n)$
3. 一共有d个特征，所以对于一层的操作，复杂度是$O(d(n\log{n}+n)) = O(dn\log{n})$
4. 该树的深度为k，所以总复杂度是$O(kdn*\log{n})$
注意事项
1. 这种方法并行效率很低，sklearn里面就是这种算法，xgboost的单线程版本也是这个方式
2. 对树节点继续分割时，需要按照某个特征值进行排序。那么对于无序的类别变量，就必须进行one-hot编码。不然某个特征是A\B\C三类，我们比较时候，就会只考虑左子树为AB或者右子树为BC，或者不分割，实际上缺少了左子树为BC的可能性
3. 因为Gain的计算与特征值无关，它采用的是已经生成的树的结构和权重（用来计算g和h），所以不需要对特征进行归一化处理

[2]. Approximate Algorithm For SPLIT FINDING

根据Basic Exact Greedy Algorithm算法，我们可以发现模型对特征中值的范围不敏感，只对顺序敏感。举个栗子，假设一个样本集合中某特征出现的值为1, 4, 6, 7，那么把它换为1, 2, 3, 4，生成的树的结构是完全一样的，只不过是对应的判断条件改变了，比如把小于6换成了小于3而已。这也给我们一个启示，我们完全可以用比例作为基础来构造模型。

Approximate-Algorithm-for-Split-Finding

很直观的，切割分割点比例的选择有两种：

全局选择：学习每棵树前，提出候选切分点。在最开始选好，然后每次分离都不变，即在总样本中选最大最小值；
局部选择：每次分裂前，重新提出候选切分点。每次分离后在分离的样本中选，即在前文所定义的叶子节点样本$I_j$中选。

可以看出，局部选择相对繁琐些，但效果会比方法1好些。

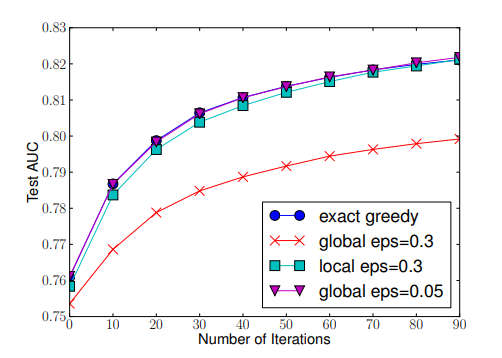
exp-Split-Finding

最后给出这几种Split-Finding方法的实验比较，可以看到局部选择比全局选择优秀的多。另外，近似算法几乎和贪婪算法差不多。

1. 普通分位数分割点

一般的，一个特征的分位数可以用来均匀的当作候选分割点。

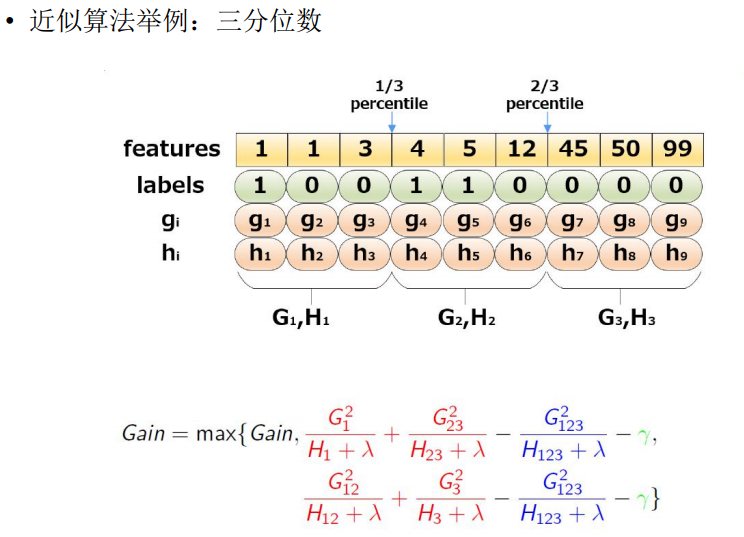
example-Approximate-percentile

2. Weighted Quantile Sketch

实际中，XGBoost不是简单地按照样本个数进行分位，而是以二阶导数值作为权重(Weighted Quantile Sketch)。假设用$D_k = {(x_1k,h_1), (x_2k,h2),(x_3k,h_3), \cdots, (x_nk,h_n)}$代表每个样本的第k个特征和其对应的二阶梯度所组成的集合。其中每一个数据点都是用二阶导数$h_i$当作权重，为什么会用$h_i$呢，可以看下目标函数的变形？

$\begin{aligned} Obj^{(t)} & = \sum\limits_{i=1}^{n} \left [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i) \right ] + \Omega(f_t) + constant \\ & = \sum\limits_{i=1}^n \frac{1}{2} h_i \left(f_t(x_i) - g_i/h_i)^2 \right ) + \Omega(f_t) + constant \\ \end{aligned}$

通过变换，可以看出是一个加权的平方loss，label是$g_i/h_i$，权重是$h_i$，所以每个样本都可以用$h_i$当作权重使用。

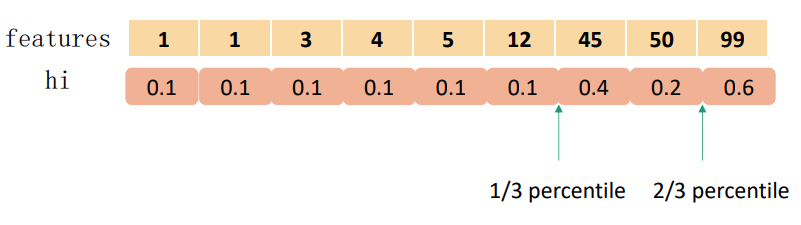
example-Weighted-Quantile-Sketch

那么就能用百分比来定义下面这个排名函数$r_k: \boldsymbol{R} \to [0,+\infty)$

$\begin{aligned} r_k(z) = \frac{1}{\sum_{(x,h)\in\boldsymbol{D_k}} h} \sum\limits_{(x,h)\in\boldsymbol{D_k}, x<z} h \end{aligned}$

上式表示的就是该特征的值小于z的样本所占总样本的比例，于是就能用下面这个不等式来寻找分离点${s_{k1}, s_{k2}, \cdots, s_{kl}}$：

$\begin{aligned} |r_k(s_{k,j}) - r_k(s_{k,j+1})| < \epsilon, \quad s_{k1}=\min\limits_i \boldsymbol{x_{ik}}, \ s_{kl}=\max\limits_i \boldsymbol{x_{ik}} \end{aligned}$

上式中$\epsilon$表示一个近似比例，或者叫做扫描步长，这意味着一共会有$1/\epsilon$个候选分割点。从最小值开始，每次增加$\epsilon * (\max\limits_i \boldsymbol{x_{ik}} - \min\limits_i \boldsymbol{x_{ik}})$作为分离点，然后在这些分离点中选择一个最大分数作为最后的分离点。

XGBoost的稀疏处理

很多机器学习的算法都是没有具体办法处理稀疏数据，如SVM，NN等。在使用模型时，经常会遇到稀疏值的问题，主要有以下几个原因：

原始数据就存在缺失；
统计特征中出现很多0；
人工构造的特征经常会有0，比如one-hot编码；

XGB训练数据的时候，它使用没有缺失的数据去进行节点分支。然后我们将特征上缺失的数据尝试放左右节点上，看缺失值应当分到那个分支节点上。我们把缺失值分配到的分支称为默认分支：

通过尝试左右分支，找到对缺失值最好的方向
仅在有值的数据点上进行分裂

Sparsity-aware-Split-Finding

XGBoost的工程设计

Column Blocks and Parallelization

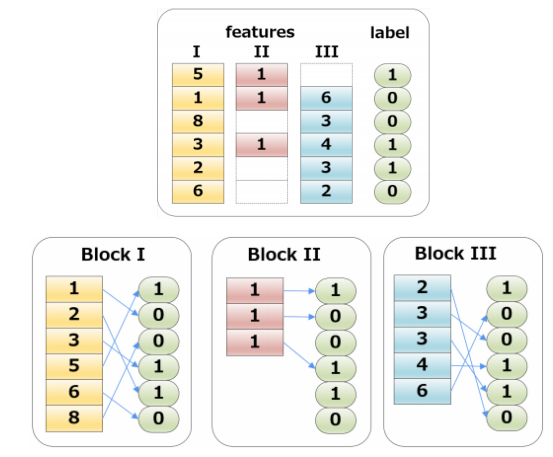
这个结构加速了split finding的过程，只需要在建树前排序一次，后面节点分裂时多线程的直接根据索引得到对应梯度信息，具体有几个点值得注意：

特征预排序，以column block的结构存于内存中
一个block可以包含一个和多个特征
样本索引（instance indices）也存储在block中
缺失值不需要存储
block中的数据以稀疏格式（CSC）存储
使用Column Blocks的方式，可以很方便的实现split finding的并行化

Column Blocks and Parallelization

Cache Aware Access

Column Blocks按特征大小顺序存储，但是这些样本的梯度信息是分散的，造成内存的不连续访问，降低CPU Cache命中率，所以XBGoost做了缓存优化方法：

pre-fetches（预取）数据到buffer中，non-continuous memory into a continuous buffer（非连续->连续），再统计梯度信息
可以调节block的大小
主线程在continuous buffer中统计梯度信息

如何上手XGBoost

讨论了这么多算法和工程的东西，还是稳扎稳打写点代码吧~

超参数配置

具体的参数配置，可以去XGBoost官网-parameters进行详细了解

General parameters
- booster: Which booster to use. Can be gbtree, gblinear or dart; gbtree and dart use tree based models while gblinear uses linear functions
- silent: 控制模型日志
- verbosity：更详细的控制模型日志
- nthread
- disable_default_eval_metric
Booster parameters
- eta：Step size shrinkage used in update to prevents overfitting
- gamma：Minimum loss reduction required to make a further partition on a leaf node of the tree
- max_depth：Maximum depth of a tree
- …
Learning task parameters
- objective: default=reg:squarederror
- base_score: The initial prediction score of all instances, global bias
- eval_metric: default according to objective
- seed：保证模型可以重现

demo代码

XGBoost现在支持Python，R，Julia，Scala等多种语言，这部分可以去XGBoost官网-get-started进行详细了解。

import xgboost as xgb

# read in data
dtrain = xgb.DMatrix('demo/data/agaricus.txt.train')
dtest = xgb.DMatrix('demo/data/agaricus.txt.test')

# specify parameters via map
param = {'max_depth':2, 'eta':1, 'objective':'binary:logistic' }
num_round = 2
bst = xgb.train(param, dtrain, num_round)

# make prediction
preds = bst.predict(dtest)

比赛利器：陈天奇的XGBoost

Index

背景

XGBoost与传统GBDT的区别

常用的符号表示

泰勒公式

XGBoost中的目标函数

总体目标函数

Regularization

Gradient Tree Boosting

XGBoost的树生成过程

问题1：最小化$Obj^{(t)}$的$w_j$

问题2：XGBoost中节点的split方法

[1]. Basic Exact Greedy Algorithm For SPLIT FINDING

[2]. Approximate Algorithm For SPLIT FINDING

XGBoost的稀疏处理

XGBoost的工程设计

Column Blocks and Parallelization

Cache Aware Access

如何上手XGBoost

超参数配置

demo代码

相关引用