GBDT初探

GBDT

背景

1999年，Friedman的论文《GREEDY FUNCTION APPROXIMATION:A GRADIENT BOOSTING MACHINE》最早提出GBDT (Gradient Boosting Decision Tree) 的思想。

到目前为止，GBDT是机器学习中一个长盛不衰的模型，其主要思想是利用弱分类器（决策树）迭代训练以得到最优模型，该模型具有训练效果好、不易过拟合等优点。GBDT 在工业界应用广泛，通常被用于点击率预测，搜索排序等任务。GBDT 也是各种数据挖掘竞赛的致命武器，据统计 Kaggle 上的比赛有一半以上的冠军方案都是基于GBDT。

机器学习基础模型

基本上所有的机器学习模型都是下面公式演化而来

$\begin{equation} \widehat{y_i} = \sum_{i=1}^{d} w_j x_{ij} \end{equation}$

上述公式中$x_0=1$，就是引入了一个偏差量，或者说加入了一个常数项。由该公式可以演化一些模型：

线性模型，最后的得分就是$\widehat{y_i}$
logistic模型，最后的得分是$\frac{1}{exp(-\widehat{y_i})}$，然后设定阈值，转为正负样本
其他的大部分模型，都在基于$\widehat{y_i}$做文章，转化为最后的分数

Boosting 思想

Boosting是一种框架算法，主要是通过对样本集的操作获得样本子集，然后用弱分类算法在样本子集上训练生成一系列的基分类器。

Boosting可以用来提高其他弱分类算法的识别率，也就是将其他的弱分类算法作为基分类算法放于Boosting框架中，通过Boosting框架对训练样本集的操作，得到不同的训练样本子集，用该样本子集去训练生成基分类器。每得到一个样本集就用该基分类算法在该样本集上产生一个基分类器，这样在给定训练轮数n后，就可产生n个基分类器，然后Boosting框架算法将这n个基分类器进行加权融合，产生一个最后的结果分类器。在这 n个基分类器中，每个单个的分类器的识别率不一定很高，但他们联合后的结果有很高的识别率，这样便提高了该弱分类算法的识别率。

Boosting系列算法最经典的包括AdaBoost算法和GBDT算法。

Boosting Tree思想

其模型 $F$ 定义为加法模型：

$\begin{equation} F(x;w) = \sum_{t=0}^{T} \alpha_t h_t(x;w_t) = \sum_{t=0}^{T} f_t(x;w_t) \end{equation}$

其中，$x$为输入样本，$h$为分类回归树（CART），$w$是分类回归树的参数，$\alpha$是每棵树的权重。
注意，在Friedman, 1999文章中，没有涉及正则项$\Omega(f_t)$这个概念。正则项的真正使用在Rie Johnson & Tong Zhang, 2014和Chen, 2016，两者大同小异，但正则项$\Omega(f_t)$的使用对于GBDT来讲有里程碑意义，它对提升训练效果非常重要。

不同的objective和最小化其的方法决定了不同种类的Boosting:

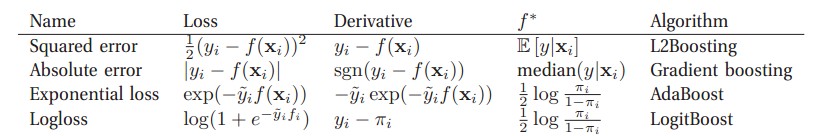
boosting-objective

GBDT是上图中的Gradient Boosting的一个子类（弱分类器为决策树）

通常，GBDT目标函数会定义为下面的形式：

$\begin{aligned} Obj = \begin{matrix} \underbrace{ \sum\limits_{i=1}^{n} L(y_i, \widehat{y_i}) } \\ {Training\ loss} \end{matrix} + \begin{matrix} \underbrace{ \sum\limits_{k=1}^{K} \Omega(f_k) } \\ {Regularization} \end{matrix} \end{aligned}$

第一项是针对 $n$ 个样本的 $Loss$, 它可以有多种选择
- 绝对值误差，$L(y_i, \widehat{y_i}) = |(y_i - \widehat{y_i})|$
- 平方误差，$L(y_i, \widehat{y_i}) = {(y_i - \widehat{y_i})}^2$，此时叫做gradient boosted machine
- logistic loss，$L(y_i, \widehat{y_i}) = y_i \ln(1 + \exp(-\widehat{y_i}) + (1-y_i)\ln(1+\exp(\widehat{y_i})))$，此时叫做logistBoost
第二项是正则项，即树的复杂度，包括叶子数量、叶子节点权重等。

原始GBDT算法框架

梯度下降和GBDT

二者都与梯度Grident有很大关系，梯度下降是在参数空间，GBDT是在函数空间，他们的形式基本一致：

Gradient-Boosting

如果将一阶参数增量换为二阶，那就基本形成了XGBoost的原理

Newton-Boosting

原始GBDT的原理

Gradient Boosting Tree

Gradient Boosting就是在函数空间的梯度下降，我们不断减去$\frac{\partial f}{\partial \theta}$，可以得到$min_{\theta} f$；同理，不断减去$\frac{\partial L}{\partial F}$，可以得到$min_{F} L$

$f_0$初始化

GBDT对初始值并不敏感，但是更好的初始值能够获得更快的收敛速度和质量，主要有以下几个方法：

随机初始化
用训练样本中的充分统计量初始化，Friedman, 1999
用其它模型的预测值初始化

训练过程

总体来说，GBDT就是一个不断拟合响应（残差）并叠加到F上的过程。在这个过程中，残差不断变小，Loss不断接近最小值。

$\tilde{y}$被成为响应(response)，它是一个和残差(redidual):$y_i - F_{k-1}(x_i)$正相关的变量，这个响应概念的提出是Friedman受到LSBoost (Least Square Boosting)的启发，在LSBoost中优化问题可以直接求得解析解，而不需要使用梯度下降，但是其中的残差恰好就是平方Loss针对函数$F(x)$的梯度（参见引用6）
上图中表达的是，使用平方误差训练一棵决策树$f_k$，拟合数据${(x_i, \tilde{y_i})}_1^N$
line search，在上一步骤中会根据平方误差得到$f_k$，这一步进行line search，让$f_k$乘以步长$\rho$后最小化$L$。这个$\rho$的出现可能让很多童鞋不理解，它到底算干嘛的。本意上是为了对模型中的每棵树进行加权，叶子节点权重算完后乘以$\rho$，起到放大$\rho$的作用。但实际中，通常将2和3两步放到一起，直接将$L \left (y_i, \widehat{y_i}^{(k-1)} + f_k(x_i) \right )$在$f_k$处进行泰勒展开，无需引入$\rho$。
将训练出来的$f_k$叠加到F